A guest blog by Sam Hassell, LandPRO
I was working with an experienced colleague a few years ago he had calculated an area of paving in a circle. Something looked wrong about the calculation to me and I asked him about it. He used the formula for the area 2π R. I asked him why he used that formula as it was wrong, he should have used πr2.
He looked at me and said; “I know that – gosh! I wonder how long I have been doing that and what has it’s impact has been”. To be fair, the language used may have been a bit more “colourful”.
My point is that we often slip into a rut in our calculations and do not realise we are making a mistake until somebody else looks or checks our calculations. The same may be said about planting calculations and the number of plants in any selected planting area. I have often had the situation when doing planting that either we do not have enough plants for a selected area as per a schedule or we have plants over.
In either case we are possibly not carrying out the design intent of the planting designer if they are not enough plants and we have had to stretch the planting distances to make it work. Alternatively, the landscape contractors’ budget may be impacted and even severely if it was the landscape contractor who made the planting calculation on numbers. The most common calculation I’ve seen f is to take the area of the planting bed and divide it by the square of the planting distance to get the number of plants. So for example, if an area is 100 square metres, and the planting distance is 500 mm, the assumption is that the area of 100 m² is divided by 0.5 * .0.5 i.e. 0.25 to give a resultant number of plants of 400.
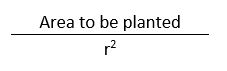
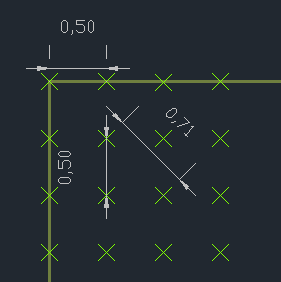
This is incorrect for the following reason. Planting distances are offset and not in a square as per the diagram below.
Below is an example of an often-used calculation – The rectangular square method. Note that the diagonal distance between plants evenly set out on a rectangular grid measures at 0.71 m.
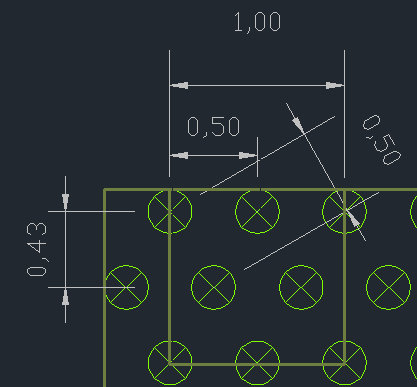
In the diagram below however, I have set out my plants on an offset grid where the distance between each plant is the required 500 mm. Note that the rectangular distance is 500 x 430 mm.
I approached a maths graduate on this and laid out the dilemma and commissioned him to calculate the correct formula based on the above criteria. If nobody objects, I’d like to refer to the formula below as the Hassall factor. It is however the ‘ Offset formula method’ It just seems appropriate that I should use my surname at last in the light of all the puns quips and comments that I often get on introducing myself – (whether you say it or just think it.)
The final formula he came up with is this:
Formula for calculating the correct no. of plants in each area; Offset formula (Hassall factor formula)
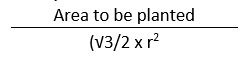
In the table below I show the difference between the rectangular (incorrect) formula Area/r² and the Hassall factor formula.
The impact on this is increased accuracy in plant numbers. And the knock-ons of unloading placement, planting and even replacements.
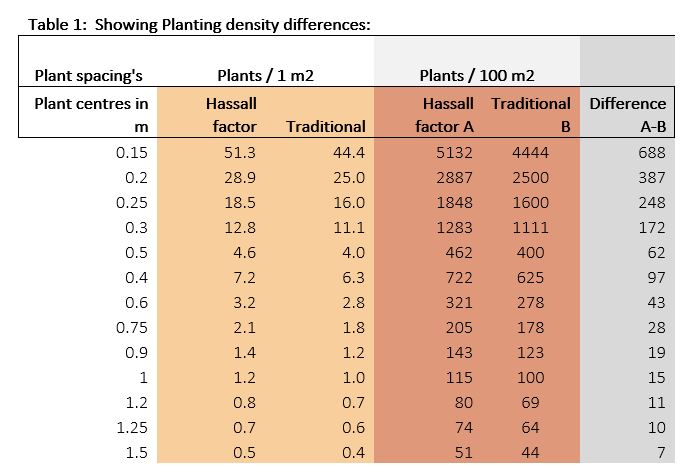
The table below shows the quantities based on the rectangular formula alongside the quantities based on the Hassall factor formula. For both 1 and 100 m2. There is a general relationship of 15.5% increase in plant numbers required. Small planting distances are often used for bedding or plug planting. The larger planting distances are often used for woodland matrix planting.
COST IMPLICATIONS
The following tables demonstrate the differences between the two systems in costs.
The implications could be experienced if a planting design was calculated giving quantities and had used the rectangular method rather than the offset method.
The following table shows the difference in supply and planting costs for different sized plants considering the following:
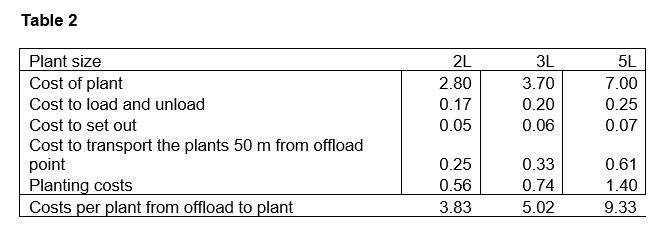
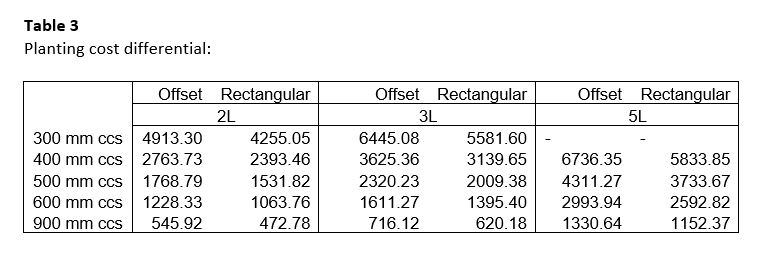
Based on the above the difference are shown in the following table for each plant size and common densities used in planting plans.
Example
If a planting area of 100 m2 were to be specified a planting distance of 400 mm centres:
From Table 1:
If the designer used a rectangular method, there would be 625 plants specified in the planting plan.
However, the required no to get best results using the offset method would be 722.
From Table 3:
The cost differential on 2L plants is:
£2763.73 and 2393.46
Difference = £376.47
The differential spread over larger areas and would have cots implications of both the designer, contractor, and the employer.
About the Author

Sam Hassall studied Civil and landscape engineering and horticulture. After years working in the contracting sector both locally and abroad, he started his cost consultancy LandPRO Ltd.
LandPRO works with both Landscape architects and garden designers as well as contractors to understand the future cost of a proposed landscape installation or to ensure profitability for contractors in a competitive tender environment.
Sam also developed the LibeRATE estimating system for landscape contractors and the Gardencosts website for garden designers.
Sam also compiles the Spon’s External works and Landscape Price book.